Extra material: Multi-product facility production

Preamble: Install Pyomo and a solver

The following cell sets and verifies a global SOLVER for the notebook. If run on Google Colab, the cell installs Pyomo and the HiGHS solver, while, if run elsewhere, it assumes Pyomo and HiGHS have been previously installed. It then sets to use HiGHS as solver via the appsi module and a test is performed to verify that it is available. The solver interface is stored in a global object SOLVER for later use.

import sys
 
if 'google.colab' in sys.modules:
    %pip install pyomo >/dev/null 2>/dev/null
    %pip install highspy >/dev/null 2>/dev/null
 
solver = 'appsi_highs'
 
import pyomo.environ as pyo
SOLVER = pyo.SolverFactory(solver)
 
assert SOLVER.available(), f"Solver {solver} is not available."

Maximizing the profit in the worst case for a multi-product facility

A common formulation for the problem of maximizing profit of a multi-product facility in a resource constrained environment is given by the following linear optimization problem:

\[\begin{split} \begin{align*} \max\ \text{profit} = \max \quad & \sum_{j\in J} c_j x_j\\ \text{s.t.} \quad & \sum_{j\in J} a_{ij}x_j \leq b_i & \forall \, i \in I\\ & x_j \geq 0 & \forall \, j\in J, \end{align*} \end{split}\]

where \(x_j\) is the production of product \(j\in J\), \(c_j\) is the net profit from producing and selling one unit of product \(j\), \(a_{i, j}\) is the amount of resource \(i\) required to product a unit of product \(j\), and \(b_i\) is amount of resource \(i\in I\) available. If this data is available, then the linear programming solution can provide a considerable of information regarding an optimal production plan and the marginal value of additional resources.

But what if coefficients of the model are uncertain? What should be the objective then? Does uncertainty change the production plan? Does the uncertainty change the marginal value assigned to resources? These are complex and thorny questions that will be largely reserved for later chapters of this book. However, it is possible to consider a specific situation within the current context.

Consider a situation where there are multiple plausible models for the net profit. These might be a result of marketing studies or from considering plant operation under multiple scenarios, which we collect in a set \(S\). The set of profit models could be written

\[ \begin{align*} \text{profit}_s & = \sum_{j} c_j^s x_j & \forall \, s\in S \end{align*} \]

where \(s\) indexes the set of possible scenarios. The scenarios are all deemed equal, no probabilistic interpretation is given.

One conservative criterion is to find maximize profit for the worst case. Letting \(z\) denote the profit for the worst case, this criterion requires finding a solution for \({x_j}\) for \({j\in J}\) that satisfies

\[\begin{split} \begin{align*} \max_{x_j} \quad & z\\ \text{s.t.} \quad & \sum_{j\in J} c_j^s x_j \geq z & \forall \, s\in S\\ & \sum_{j\in J} a_{ij}x_j \leq b_i & \forall \, i \in I\\ & x_j \geq 0 & \forall \, j\in J \end{align*} \end{split}\]

where \(z\) is lowest profit that would be encountered under any condition.

Data

We import the same data as in the previous notebook regarding the BIM production with different possible profit scenarios.

import pandas as pd

BIM_scenarios = pd.DataFrame(
    [[12, 9], [11, 10], [8, 11]], columns=["product 1", "product 2"]
)

BIM_scenarios.index.name = "scenarios"
print("\nProfit scenarios")
display(BIM_scenarios)

BIM_resources = pd.DataFrame(
    [
        ["silicon", 1000, 1, 0],
        ["germanium", 1500, 0, 1],
        ["plastic", 1750, 1, 1],
        ["copper", 4000, 1, 2],
    ],
    columns=["resource", "available", "product 1", "product 2"],
)
BIM_resources = BIM_resources.set_index("resource")

print("\nAvailable resources and resource requirements")
display(BIM_resources)

Profit scenarios

	product 1	product 2
scenarios
0	12	9
1	11	10
2	8	11

Available resources and resource requirements

	available	product 1	product 2
resource
silicon	1000	1	0
germanium	1500	0	1
plastic	1750	1	1
copper	4000	1	2

Pyomo Model

An implementation of the maximum worst-case profit model.

def maxmin(scenarios, resources):
    model = pyo.ConcreteModel("BIM production planning for worst-case profit")

    products = resources.columns.tolist()
    products.remove("available")

    model.I = pyo.Set(initialize=resources.index)
    model.J = pyo.Set(initialize=products)
    model.S = pyo.Set(initialize=scenarios.index)

    @model.Param(model.I, model.J)
    def a(m, i, j):
        return resources.loc[i, j]

    @model.Param(model.I)
    def b(m, i):
        return resources.loc[i, "available"]

    @model.Param(model.S, model.J)
    def c(m, s, j):
        return scenarios.loc[s, j]

    model.x = pyo.Var(model.J, domain=pyo.NonNegativeReals)
    model.z = pyo.Var()

    @model.Objective(sense=pyo.maximize)
    def profit(m):
        return m.z

    @model.Constraint(model.S)
    def scenario_profit(m, s):
        return m.z <= sum(m.c[s, j] * m.x[j] for j in m.J)

    @model.Constraint(model.I)
    def resource_limits(m, i):
        return sum(m.a[i, j] * m.x[j] for j in m.J) <= m.b[i]

    return model


m = maxmin(BIM_scenarios, BIM_resources)
SOLVER.solve(m)

worst_case_profit = m.profit()
print("\nWorst case profit =", worst_case_profit)

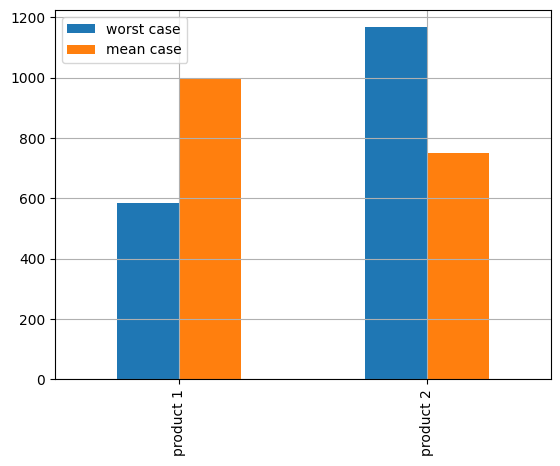
worst_case_plan = pd.Series({j: m.x[j]() for j in m.J}, name="worst case")
print(f"\nWorst case production plan:")
display(worst_case_plan)

Worst case profit = 17500.0

Worst case production plan:

product 1     583.33333
product 2    1166.66670
Name: worst case, dtype: float64

Optimizing for the mean scenario

Is maximizing the worst case a good idea? Maximizing the worst case among all cases is a conservative planning outlook. It may be worth investigating alternative planning outlooks.

The first step is to create a model to optimize a single scenario. Without repeating the mathematical description, the following Pyomo model is simply the maxmin model adapted to a single scenario.

def max_profit(scenario, resources):
    model = pyo.ConcreteModel("BIM")

    products = resources.columns.tolist()
    products.remove("available")

    model.I = pyo.Set(initialize=resources.index)
    model.J = pyo.Set(initialize=products)

    @model.Param(model.I, model.J)
    def a(m, i, j):
        return resources.loc[i, j]

    @model.Param(model.I)
    def b(m, i):
        return resources.loc[i, "available"]

    @model.Param(model.J)
    def c(m, j):
        return scenario[j]

    model.x = pyo.Var(model.J, domain=pyo.NonNegativeReals)
    model.z = pyo.Var()

    @model.Objective(sense=pyo.maximize)
    def profit(m, s):
        return sum(m.c[j] * m.x[j] for j in m.J)

    @model.Constraint(model.I)
    def resource_limits(m, i):
        return sum(m.a[i, j] * m.x[j] for j in m.J) <= m.b[i]

    return model

The next cell computes the optimal plan for the mean scenario.

# create mean scenario
mean_case = max_profit(BIM_scenarios.mean(), BIM_resources)
SOLVER.solve(mean_case)

mean_case_profit = mean_case.profit()
mean_case_plan = pd.Series({j: mean_case.x[j]() for j in mean_case.J}, name="mean case")

print(f"\nMean case profit = {mean_case_profit:0.1f}")
print("\nMean case production plan:")
print(mean_case_plan)

Mean case profit = 17833.3

Mean case production plan:
product 1    1000.0
product 2     750.0
Name: mean case, dtype: float64

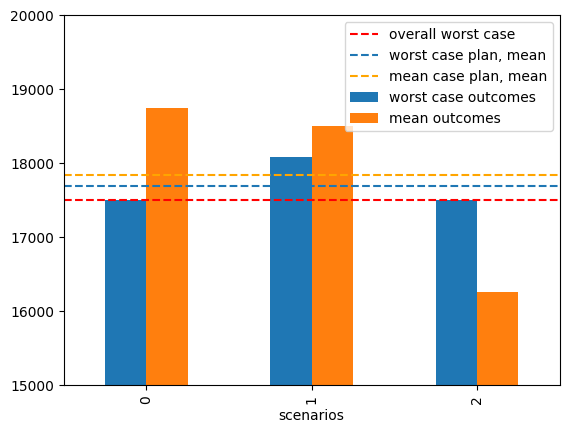
The expected profit under the mean scenario if 17833 which is 333 greater than for the worst case. Also note the production plan is different.

Which plan should be preferred? The one that produces a guaranteed profit of 17500 under all scenarios, or one that produces expected profit of 17833?

mean_case_outcomes = BIM_scenarios.dot(mean_case_plan)
mean_case_outcomes.name = "mean outcomes"

worst_case_outcomes = BIM_scenarios.dot(worst_case_plan)
worst_case_outcomes.name = "worst case outcomes"

ax = pd.concat([worst_case_outcomes, mean_case_outcomes], axis=1).plot(
    kind="bar", ylim=(15000, 20000)
)
ax.axhline(worst_case_profit, linestyle="--", color="red", label="overall worst case")
ax.axhline(worst_case_outcomes.mean(), linestyle="--", label="worst case plan, mean")
ax.axhline(
    mean_case_outcomes.mean(),
    linestyle="--",
    color="orange",
    label="mean case plan, mean",
)
ax.legend()

ax = pd.concat([worst_case_plan, mean_case_plan], axis=1).plot(kind="bar", grid=True)

Summary

Planning for the worst case reduces the penalty of a bad outcome. But it comes at the cost of reducing the expected payout, the also the maximum payout should the most favorable scenario occur.

1. Which plan would you choose. Why?

2. Make a case for the other choice.